Service: Grid filling and extending help when a dataset is incomplete

DATA gaps in and around geophysical and other data grids often need filling. Popular methods currently in use have survived largely unchanged for decades. But given the increasing interest in segmentation and structural analyses of these datasets, gap-filling methods within the minerals exploration industry are likely due for a shake-up.
Not all geophysical datasets have perfect data coverage.
Often, areas containing multiple 'postage-stamp' airborne surveys that have been stitched together contain significant corridors where survey boundaries fail to overlap. These corridors are data gaps. Interpolation should be done on those areas, to come up with acceptable stand-in values.
As well, airborne geophysical surveys rarely delineate single, perfect quadrangles.
In fact survey boundaries sometimes resemble the staircases of an M.C. Escher lithograph. This means data must be extrapolated to form a simple-shaped survey boundary before any sort of frequency-domain data analysis can be started (e.g., reduction to the pole, first vertical derivative, pseudogravity, segmentation, structure detection, and 'worming').
Of course, interpolated and extrapolated data are not actual, measured data. Rather, interpolation and extrapolation are data-simulation procedures. The way in which a simulation is done — and the quality of the stand-in data produced — can therefore significantly affect subsequent data processing, imaging and interpretation.Currently, interpolation and extrapolation methods seem to be regarded within geophysics circles as relatively routine and uncontroversial.
Methods commonly used in the minerals exploration industry include natural neighbors [1], maximum entropy spectrum analysis [2], and minimum curvature [3]. They typically hark back at least as far as the 1970s and 1980s and since then have gone through relatively little change.
However, in disciplines heavily involved in spatial and time-series data, dataset extension and gap-filling methods have been exploring other avenues. For instance, methods mentioned among papers on environmental, astrophysical, and remote-sensing research, have included the resurrected Lomb-Scargle periodogram [4], a new adaptation of singular spectrum analysis for use in magnetosphere studies [5], and the Ising spin model, which was borrowed from the discipline of statistical physics [6].
We think the benefits of this rapid expansion of concepts in data simulation will eventually spill over into applications for exploration geophysics datasets.
Generally speaking, Fathom Geophysics' interpolation and extrapolation procedure uses the measured data to "train" a data-simulation filter. The measured data can be expressed as a spectrum, and the overall aim is to have the simulated data possess the same spectral characteristics as the measured data. In other words, the simulated data should ideally look like the measured data and behave in the same way during image processing.
The optimal filter for the particular dataset concerned is then arrived at iteratively in a multi-scale fashion (various levels of coarseness). It's the filter that will do the best job of deconvolving the measured data.*
Points to note about Fathom Geophysics' current grid-filling and grid-extension technique include:
- Our stand-in values incorporate long and short wavelengths and are determined in two dimensions simultaneously. Compare this with typical standard treatments, in which often only one dimension is processed at a time, and in which either long or short wavelengths are often lost, depending on the method used.
- For magnetic datasets, our simulated long-wavelength features will be carried into the measured data during reduction to the pole. We think that any important, large-scale feature that is clearly continuing through an area should be incorporated in any data gaps, so that this type of feature remains detectable in structural analyses done after RTPing. You don't want these features artifically truncated just because your data contains gaps.
- While computation times are longer than for standard treatments, we think this is time well spent.
- When interpolation is being done, if too much data is missing, then reliable stand-in values cannot be simulated. (This is not so much of an issue when extending a grid outward.)
We've come up with two examples to illustrate the stark differences among different grid-filling and extension methods. The first example shows airborne magnetic data in the Musgrave region of Western Australia. The second example shows topography data at Ruby Mountains in Nevada, USA.
The resulting images speak for themselves. Without further ado, here they are (below).
 FIGURE 1: Original measured airborne magnetic data in reduced-to-the-pole (RTP) form for the Musgrave region, Western Australia. Note the survey's stepped boundaries.
FIGURE 1: Original measured airborne magnetic data in reduced-to-the-pole (RTP) form for the Musgrave region, Western Australia. Note the survey's stepped boundaries.
 FIGURE 2: White banding showing where a gap was 'punched' into the original measured airborne magnetic data in reduced-to-the-pole (RTP) form for the Musgrave region, Western Australia.
FIGURE 2: White banding showing where a gap was 'punched' into the original measured airborne magnetic data in reduced-to-the-pole (RTP) form for the Musgrave region, Western Australia.
 FIGURE 3: Results of Fathom Geophysics' treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap we 'punched' into the data, and grid-extension allowed us to create a simple, rectangular survey boundary.
FIGURE 3: Results of Fathom Geophysics' treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap we 'punched' into the data, and grid-extension allowed us to create a simple, rectangular survey boundary.
 FIGURE 4: Results of Fathom Geophysics' treatment of the gapped Musgrave dataset, with the original survey boundaries restored.
FIGURE 4: Results of Fathom Geophysics' treatment of the gapped Musgrave dataset, with the original survey boundaries restored.
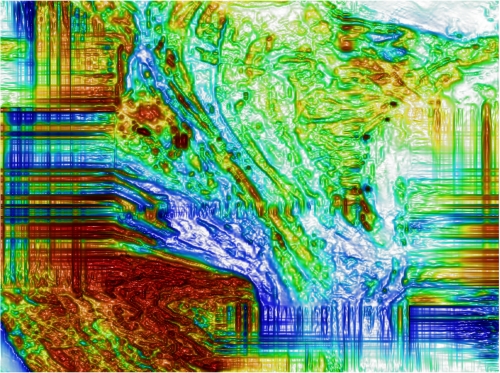 FIGURE 5: Results of a current industry-standard treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap 'punched' into the data, and grid-extension created a simple, rectangular survey boundary.
FIGURE 5: Results of a current industry-standard treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap 'punched' into the data, and grid-extension created a simple, rectangular survey boundary.
 FIGURE 6: Results of a current industry-standard treatment of the gapped Musgrave dataset, with the original survey boundaries restored. Note the infill data's striated appearance in these areas.
FIGURE 6: Results of a current industry-standard treatment of the gapped Musgrave dataset, with the original survey boundaries restored. Note the infill data's striated appearance in these areas.
 FIGURE 7: Results of minimum curvature treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap 'punched' into the data, and grid-extension created a simple, rectangular survey boundary.
FIGURE 7: Results of minimum curvature treatment of the gapped Musgrave dataset. Grid-filling closed the internal gap 'punched' into the data, and grid-extension created a simple, rectangular survey boundary.
 FIGURE 8: Results of minimum curvature treatment of the gapped Musgrave dataset, with the original survey boundaries restored. Note the infill data's flattened appearance in these areas.
FIGURE 8: Results of minimum curvature treatment of the gapped Musgrave dataset, with the original survey boundaries restored. Note the infill data's flattened appearance in these areas.
 FIGURE 9: Original measured topographic data in the region of the Ruby Mountains, Nevada.
FIGURE 9: Original measured topographic data in the region of the Ruby Mountains, Nevada.
 FIGURE 10: White banding showing where a gap was 'punched' into the original measured topographic data in the region of the Ruby Mountains, Nevada.
FIGURE 10: White banding showing where a gap was 'punched' into the original measured topographic data in the region of the Ruby Mountains, Nevada.
 FIGURE 11: Results of Fathom Geophysics' treatment of the gapped Ruby Mountains dataset.
FIGURE 11: Results of Fathom Geophysics' treatment of the gapped Ruby Mountains dataset.
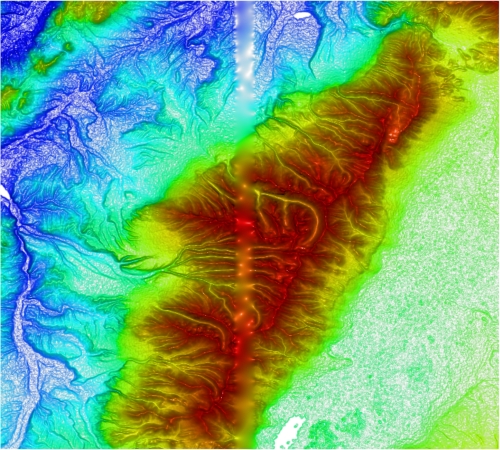 FIGURE 12: Results of minimum curvature treatment of the gapped Ruby Mountains dataset. Note the infill data's flattened appearance in these areas.
FIGURE 12: Results of minimum curvature treatment of the gapped Ruby Mountains dataset. Note the infill data's flattened appearance in these areas.
References and notes
* The measured data we see in a dataset has been pushed around by unseen natural processes. The technical term for this pushing around is 'convolution'. To predict or simulate data, we want to get back to the original signal — the signal as it existed before being 'convolved'. That is, we want to deconvolve the measured data.
[1] D.F. Watson (1988) "Natural neighbor sorting on the n-dimensional sphere", Pattern Recognition, 21, 1, 63-67.
[2] See, for example, references cited in: T.J. Ulrych (1972) "Maximum entropy power spectrum of truncated sinusoids", Journal of Geophysical Research, 77, 8, 1396-1400.
[3] I.C. Briggs (1974) "Machine contouring using minimum curvature", Geophysics, 39, 1, 39-48.
[4] K. Hocke and N. Kampfer (2009) "Gap filling and noise reduction of unevenly sampled data by means of the Lomb-Scargle periodogram", Atmospheric Chemistry and Physics, 9, 4197-4206.
[5] D. Kondrashov and M. Ghil (2006) "Spatio-temporal filling of missing data in geophysical data sets", Nonlinear Processes in Geophysics, 13, 2,151-159.
[6] M. Zukovic and D.T. Hristopulos (2008) "An algorithm for spatial data classification and automatic mapping based on 'spin' correlations", In: Proceedings of the 22nd European Conference on Modeling and Simlulation, 7 pages.
